• Pyslvs 中的三角形表示式
• Python 版本的原始碼

Pyslvs 三角形表示式

為了達成機構路徑的模擬，以符合 PMKS 所能模擬的接頭種類，Pyslvs 採用三種幾何解法：

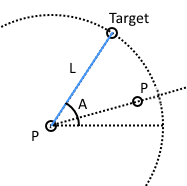
• PLA(P)：透過兩個（或一個）已知點、基準點至目標點距離，及其（與水平線）的夾角，可以求得目標點座標。
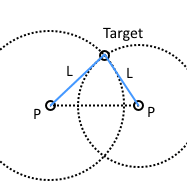
• PLLP：透過兩個已知點、兩基準點至目標點距離，可以求得目標點座標。
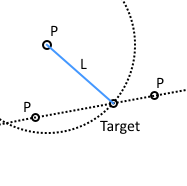
• PLPP：透過一個已知點、基準點至目標點距離、已知兩點連成的直線，可以求得目標點在直線上的座標。

PLAP

PLLP

PLPP

表示式

Pyslvs 使用函式解題的表示法如下：

Function[parameter0, parameter1, parameter2, ...](Target); ...

當透過輸入端求解之後，可以透過解出的目標點繼續求解。

例如，一個四連桿機構可以透過三個函式求解：

#Known: a0, P0, P2, L0, L1, L2, L3, L4
PLAP[P0, L0, a0](P1); PLLP[P1, L1, L2, P2](P3); PLLP[P1, L3, L4, P3](P4)

原始碼

這裡提供 Cython 的輸入輸出類型與 Python 版本的運算方法。

PLAP

tuple PLAP(Coordinate A, double L0, double a0, Coordinate B=0, bool inverse=false);

def PLAP(A, L0, a0, B=None, inverse=False):
    """Point on circle by angle."""
    a1 = atan2(B.y - A.y, B.x - A.x) if B else 0
    if inverse:
        return (A.x + L0*cos(a1 - a0), A.y + L0*sin(a1 - a0))
    else:
        return (A.x + L0*cos(a1 + a0), A.y + L0*sin(a1 + a0))

PLLP

tuple PLLP(Coordinate A, double L0, double L1, Coordinate B, bool inverse=false);

def PLLP(A, L0, L1, B, inverse=False):
    """Two intersection points of two circles."""
    dx = B.x - A.x
    dy = B.y - A.y
    d = A.distance(B)

    #No solutions, the circles are separate.
    if d > L0 + L1:
        return (nan, nan)

    #No solutions because one circle is contained within the other.
    if d < abs(L0 - L1):
        return (nan, nan)

    #Circles are coincident and there are an infinite number of solutions.
    if (d == 0) and (L0 == L1):
        return (nan, nan)
    a = (L0*L0 - L1*L1 + d*d)/(2*d)
    h = sqrt(L0*L0 - a*a)
    xm = A.x + a*dx/d
    ym = A.y + a*dy/d

    if inverse:
        return (xm + h*dy/d, ym - h*dx/d)
    else:
        return (xm - h*dy/d, ym + h*dx/d)

PLPP

tuple PLPP(Coordinate A, double L0, Coordinate B, Coordinate C, bool inverse=false);

def PLAP(A, L0, B, C, inverse=False):
    """Two intersection points of a line and a circle."""
    line_mag = B.distance(C)
    dx = C.x - B.x
    dy = C.y - B.y
    u = ((A.x - B.x)*dx + (A.y - B.y)*dy) / (line_mag*line_mag)
    I = Coordinate(B.x + u*dx, B.y + u*dy)

    #Test distance between point A and intersection.
    d = A.distance(I)
    if d > L0:
        #No intersection.
        return (nan, nan)
    elif d == L0:
        #One intersection point.
        return (I.x, I.y)

    #Two intersection points.
    d = sqrt(L0*L0 - d*d) / line_mag
    dx *= d
    dy *= d
    if inverse:
        return (I.x - dx, I.y - dy)
    else:
        return (I.x + dx, I.y + dy)