Pyslvs 開發進度
- 運算進度條
- 不同演算法參數調整
- tinycadlib 更新
運算進度條
透過論壇的小技巧製作出可以回傳 Cython 進度的方式(適用於所有 Python function)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | cdef class Genetic(object): """宣告""" cdef object progress_fun def __cinit__(self, #其他參數 object progress_fun=None): #將 progress_fun 放到 self 中 self.progress_fun = progress_fun cpdef run(self): #每代的迴圈 for self.gen in range(1, self.maxGen + 1): """計算流程""" #計算後回傳當前代數 if self.progress_fun is not None: self.progress_fun(self.gen) |
在 Python 端只要為 QThread 建立信號 progress_update,並將信號的 emit 方法傳入 Cython Object 即可。
class WorkerThread(QThread):
progress_update = pyqtSignal(int)
def generateProcess(self):
#選擇演算法並改名成 foo
self.fun = foo(mechanismObj, progress_fun=self.progress_update.emit, **APs)
time_and_fitness, fitnessParameter = self.fun.run()
此信號在 GUI 中與 Progress bar 的 setValue 信號槽連接即可。
self.work.progress_update.connect(self.progressBar.setValue)
接著就能看到當前運算的進度了,上述方法只須記得統一用 int 類型即可。
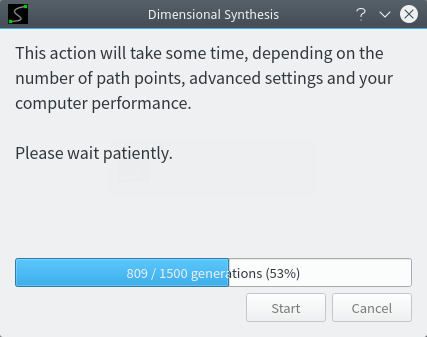
不同演算法參數調整
後來發現,若是 Firefly 的代數與初始族群較大,將會比其他演算法花更久的時間,因此做了初始族群的調整。
初始族群的數量只比學長預設的多 1 倍即可。
- 基因演算法由 250 提昇為 500。
- 螢火蟲演算法由 40 提昇為 80。
- 差分演化法由 190 提昇為 400。
tinycadlib 更新
大致了解 Cython 語法後,為 tinycadlib 程式庫新增了三角形驗證函式 legal_triangle 和 PLPP 計算式。
前者是因為之前的 build_planar object function 似乎沒有邊長驗證機制,導致產出非三角形的連桿組;加入後還在觀察情況是否會改善。
1 2 3 4 5 6 | cpdef bool legal_triangle(Coordinate A, Coordinate B, Coordinate C): #L0, L1, L2 is triangle cdef double L0 = A.distance(B) cdef double L1 = B.distance(C) cdef double L2 = A.distance(C) return L1+L2>L0 and L0+L2>L1 and L0+L1>L2 |
後者則是備用於滑塊演算法的需求。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | cpdef PLPP(Coordinate A, double L0, Coordinate B, Coordinate C, double loop=1): cdef double x1 = A.x cdef double y1 = A.y cdef double x2 = B.x cdef double y2 = B.y cdef double x3 = C.x cdef double y3 = C.y if loop>0: return ( ((x2-x3)*(x1*x2*y2 - x1*x2*y3 - x1*y2*x3 + x1*x3*y3 + y1*y2**2 - 2*y1*y2*y3 + y1*y3**2 + x2**2*y3 - x2*y2*x3 - x2*x3*y3 + y2*x3**2 + (-y2 + y3)*sqrt(L0**2*x2**2 - 2*L0**2*x2*x3 + L0**2*y2**2 - 2*L0**2*y2*y3 + L0**2*x3**2 + L0**2*y3**2 - x1**2*y2**2 + 2*x1**2*y2*y3 - x1**2*y3**2 + 2*x1*y1*x2*y2 - 2*x1*y1*x2*y3 - 2*x1*y1*y2*x3 + 2*x1*y1*x3*y3 - 2*x1*x2*y2*y3 + 2*x1*x2*y3**2 + 2*x1*y2**2*x3 - 2*x1*y2*x3*y3 - y1**2*x2**2 + 2*y1**2*x2*x3 - y1**2*x3**2 + 2*y1*x2**2*y3 - 2*y1*x2*y2*x3 - 2*y1*x2*x3*y3 + 2*y1*y2*x3**2 - x2**2*y3**2 + 2*x2*y2*x3*y3 - y2**2*x3**2)) - (x2*y3 - y2*x3)*(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2))/((y2 - y3)*(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2)), (x1*x2*y2 - x1*x2*y3 - x1*y2*x3 + x1*x3*y3 + y1*y2**2 - 2*y1*y2*y3 + y1*y3**2 + x2**2*y3 - x2*y2*x3 - x2*x3*y3 + y2*x3**2 + (-y2 + y3)*sqrt(L0**2*x2**2 - 2*L0**2*x2*x3 + L0**2*y2**2 - 2*L0**2*y2*y3 + L0**2*x3**2 + L0**2*y3**2 - x1**2*y2**2 + 2*x1**2*y2*y3 - x1**2*y3**2 + 2*x1*y1*x2*y2 - 2*x1*y1*x2*y3 - 2*x1*y1*y2*x3 + 2*x1*y1*x3*y3 - 2*x1*x2*y2*y3 + 2*x1*x2*y3**2 + 2*x1*y2**2*x3 - 2*x1*y2*x3*y3 - y1**2*x2**2 + 2*y1**2*x2*x3 - y1**2*x3**2 + 2*y1*x2**2*y3 - 2*y1*x2*y2*x3 - 2*y1*x2*x3*y3 + 2*y1*y2*x3**2 - x2**2*y3**2 + 2*x2*y2*x3*y3 - y2**2*x3**2))/(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2) ) else: return ( ((x2-x3)*(x1*x2*y2 - x1*x2*y3 - x1*y2*x3 + x1*x3*y3 + y1*y2**2 - 2*y1*y2*y3 + y1*y3**2 + x2**2*y3 - x2*y2*x3 - x2*x3*y3 + y2*x3**2 + (y2 - y3)*sqrt(L0**2*x2**2 - 2*L0**2*x2*x3 + L0**2*y2**2 - 2*L0**2*y2*y3 + L0**2*x3**2 + L0**2*y3**2 - x1**2*y2**2 + 2*x1**2*y2*y3 - x1**2*y3**2 + 2*x1*y1*x2*y2 - 2*x1*y1*x2*y3 - 2*x1*y1*y2*x3 + 2*x1*y1*x3*y3 - 2*x1*x2*y2*y3 + 2*x1*x2*y3**2 + 2*x1*y2**2*x3 - 2*x1*y2*x3*y3 - y1**2*x2**2 + 2*y1**2*x2*x3 - y1**2*x3**2 + 2*y1*x2**2*y3 - 2*y1*x2*y2*x3 - 2*y1*x2*x3*y3 + 2*y1*y2*x3**2 - x2**2*y3**2 + 2*x2*y2*x3*y3 - y2**2*x3**2)) - (x2*y3 - y2*x3)*(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2))/((y2 - y3)*(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2)), (x1*x2*y2 - x1*x2*y3 - x1*y2*x3 + x1*x3*y3 + y1*y2**2 - 2*y1*y2*y3 + y1*y3**2 + x2**2*y3 - x2*y2*x3 - x2*x3*y3 + y2*x3**2 + (y2 - y3)*sqrt(L0**2*x2**2 - 2*L0**2*x2*x3 + L0**2*y2**2 - 2*L0**2*y2*y3 + L0**2*x3**2 + L0**2*y3**2 - x1**2*y2**2 + 2*x1**2*y2*y3 - x1**2*y3**2 + 2*x1*y1*x2*y2 - 2*x1*y1*x2*y3 - 2*x1*y1*y2*x3 + 2*x1*y1*x3*y3 - 2*x1*x2*y2*y3 + 2*x1*x2*y3**2 + 2*x1*y2**2*x3 - 2*x1*y2*x3*y3 - y1**2*x2**2 + 2*y1**2*x2*x3 - y1**2*x3**2 + 2*y1*x2**2*y3 - 2*y1*x2*y2*x3 - 2*y1*x2*x3*y3 + 2*y1*y2*x3**2 - x2**2*y3**2 + 2*x2*y2*x3*y3 - y2**2*x3**2))/(x2**2 - 2*x2*x3 + y2**2 - 2*y2*y3 + x3**2 + y3**2) ) |
Comments
comments powered by Disqus