每星期創意性機構設計課程筆記整理

• 類型合成
• 自由度
• 心得

類型合成

類型合成 (Type Synthesis) 的合成對象是「機構類型」，機構類型可以透過如下參數定義：

• Degree of Freedom 自由度 (Dof)
• Number of Link 桿件數 (NL)
• Type / Number of Joint 接頭種類 / 接頭數 (J)

其中桿件數 (NL) 和接頭 (J) 可以求得自由度 (Dof)，這在下一小節會提到。

機構類型並不包含接點位置或連桿長度等數據，僅僅是代表這種機構的特色，如輸入端、連桿與不同接頭的數量。

舉例來說，曲柄搖桿是四連桿尺寸的一種，桿件數為 4，有 4 個旋轉接頭；平行四連桿、雙搖桿或雙曲柄也是如此，它們即為同一種機構類型。

泰奧．揚森 (Theo Jansen) 的八連桿雖然作動上與四連桿相似，不過桿件數為 8，10 個旋轉接頭，並不屬於同一種連桿。

類型合成的目的在於從現有的存在設計 (Exist Design) 跳脫成新設計 (New Design)，以取得新的專利 (patent)。

自由度

以數學模型的角度，自由度 (Degree of Freedom) 是連桿組的獨立變數的數量。換而言之，當給定輸入端的數目，可以得到此連桿組狀態的唯一解。

連桿組一般稱為運動鍊 (Kinematic chain)，當其中一個桿件作為機架（主座標系）時，此連桿組可謂拘束化 (Constrained)，稱為機構。

平面系統

平面系統中，物體的全自由度為 3，為 x、y 座標的增量與 z 軸的旋轉量，當配合接頭後，會將各桿件的自由度減少。

$$Dof=3(N_{L}-1)-2\times{J_{R}}-2\times{J_{P}}-1\times{J_{G}}-1\times{J_{RP}}$$

首先將各桿件的全自由度相加，接著將各種接頭失去的自由度減去。

• R 為旋轉對，失去平移的自由度，因此扣 2。
• P 為滑動對，失去旋轉與單方向移動，因此扣 2。
• G 為齒輪對，為旋轉與滑動，失去單方向移動，因此扣 1。
• PMKS 的 RP 為槽中銷，為旋轉與滑動，失去單方向移動，因此扣 1。

P 和 RP 的差異在於 P 多了一個滑塊，而滑塊屬於桿件，如圖所示：

下圖的桿件數為 4，R 接頭為 3 個，P 接頭為 1 個。（PMKS Server）

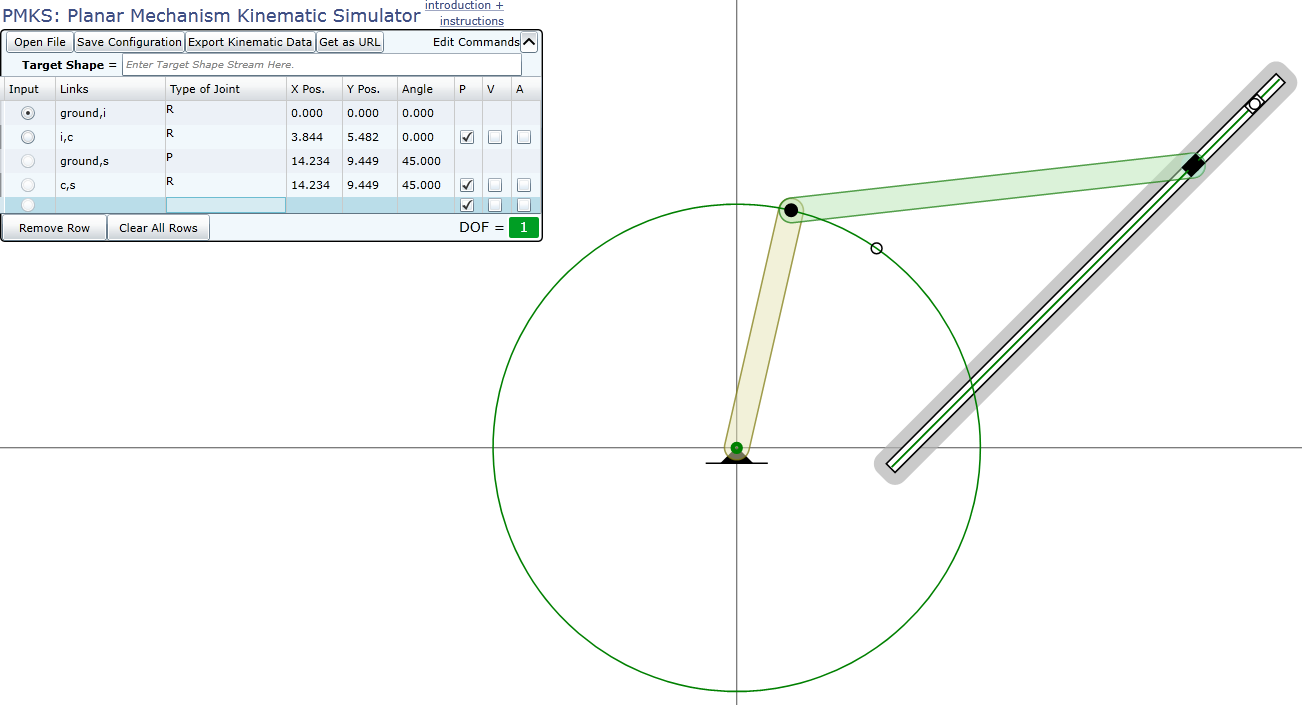
下圖的桿件數為 3，R 接頭為 2 個，RP 接頭為 1 個。（PMKS Server）

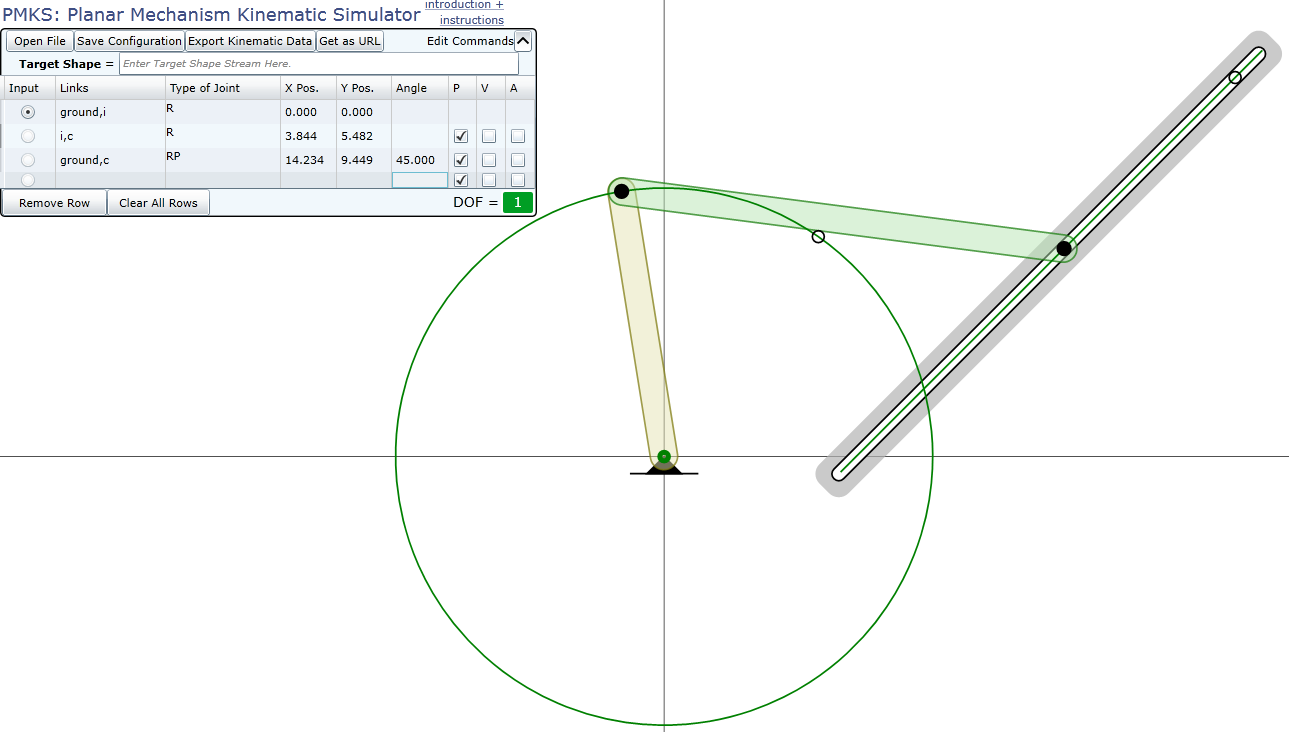
透過自由度可證，當自由度小於 1 時，會無法接收任何輸入。

但是有些連桿雖然自由度低於 1，在某些情況下是可以使用的，例如平行搖桿：

下圖的桿件數為 5，R 接頭為 6 個。（PMKS Server）

Solvespace 這裡有時求的到解，有時會紅屏。

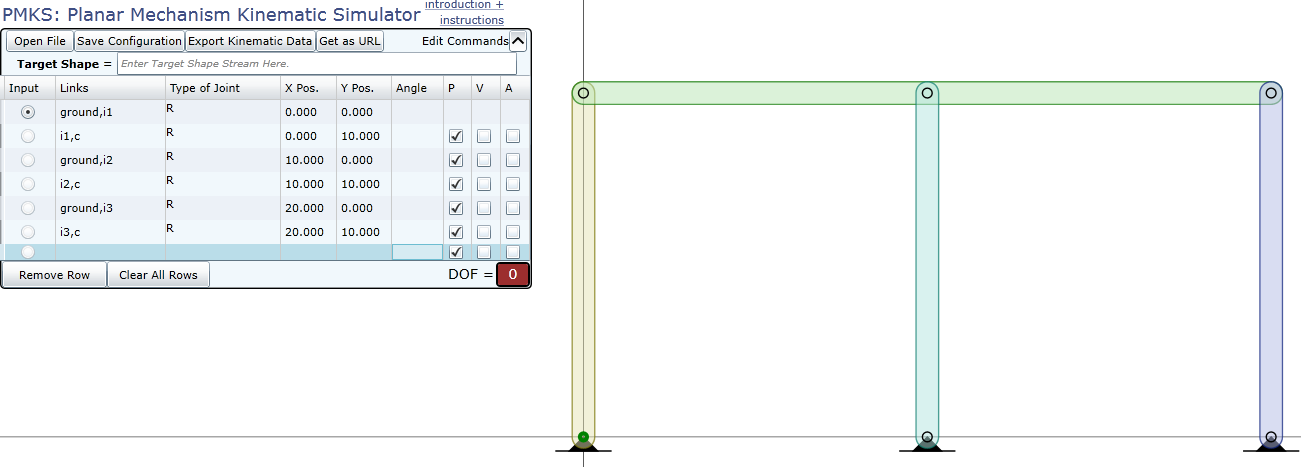
空間系統

空間系統的全自由度為 6，為 x、y、z 軸的增量與旋轉。

$$Dof=6(N_{L}-1)-5\times{J_{R}}-5\times{J_{P}}-3\times{J_{S}}$$

原本的接頭繼承自平面機構，因此 R 和 P 接頭只釋出 1 個自由度，其他接頭也是同理。

在空間系統中，還有更多樣的接頭：

• S 為球接頭 (Spherical)，只有旋轉的 3 個自由度。
• 螺旋接頭，有兩種運動方式，但是彼此為相依關係 S(θ)，因此自由度為 1，同 P 接頭。

當一桿件兩端皆為 S 接頭時，如 Delta 3D 列印機的連桿，會產生自轉，不過此自轉對整個系統是沒任何影響的，稱為贅餘 (Redundent) 自由度，計算時應當扣除。

如下面的 6 對史都華連桿計算，桿件數為 14，P 接頭為 6 個，S 接頭為 12 個：

$$Dof=6(14-1)-5\times{0}-5\times{6}-3\times{12}=6+6(自轉)$$

輸入為 6 個 P 接頭。

心得

排除特殊連桿，希望 Pyslvs 可以根據自由度的數量，讓使用者選擇從指定的接頭輸入，而 Path track 功能則變為 Solvespace 單純紀錄路徑的功能。

存下來的路徑，可以套用至以前的 demo 功能，類似錄製性的可以重新播放。

接頭輸入系統即為之前的 Drive shaft，可能需要重新設計，P 和 RP 接頭若也要接收輸入，則需規劃一下。